مرکز تحلیل آماری نوین
تجزیه و تحلیل آماری رساله دکتری، پایان نامه و مقاله های علمی
آخرین مطالب
- ۹۹/۰۵/۱۴انجام تحلیل با روش معادلات ساختاری
- ۹۵/۰۹/۱۰تحلیل خوشه ای
- ۹۵/۰۹/۰۴تحلیل تشخیصی
- ۹۵/۰۹/۰۴مدلیابی معادلات ساختاری
- ۹۵/۰۸/۱۷تعـریف متغیرها و وارد کردن داده ها
طبقه بندی موضوعی
- معرفی مرکز تحلیل آماری نوین (۳)
- همایش های علمی (۱۸)
- طراحی پرسشنامه (۴)
-
برآورد تعداد نمونه (۹)
- دپارتمان آموزش (۷۳)
در نمونه گیری طبقه ای، واحدهای جامعه مورد مطالعه در طبقه هایی که از نظر صفت متغیر همگن تر هستند، گروه بندی می شوند. به این ترتیب تغییرات در درون گروه ها حداقل می شود معمولا برای طبقه بندی واحدهای جامعه، متغیری به عنوان ملاک در نظر گرفته می شود که با صفت متغیر مورد مطالعه بستگی داشته باشد.
برای مثال به منظور بررسی نسبت قبول شدگان در پایه پنجم ابتدایی در شهر تهران و رابطه آن با محل جغرافیایی دبستان، می توان دبستان های شهر تهران را برحسب محل آن ها به پنج طبقه تقسیم کرد. طبقه اول دبستان های شمال غربی، طبقه دوم دبستان های شمال شرقی، طبقه سوم دبستان های مرکزی، طبقه چهارم دبستان های جنوب غربی و طبقه پنجم دبستان های جنوب شرقی. پس از آن از هر طبقه تعدادی دبستان به روش تصادفی ساده انتخاب می شود.
در نمونه گیری طبقه ای حجم نمونه n را به شیوه های مختلف می توان میان طبقات تقسیم کرد. ساده ترین شیوه تقسیم مساوی تعداد نمونه میان طبقات است. سایر شیوه ها شامل انتساب بهینه و انتساب متناسب می باشند.
برآورد میانگین جامعه :
برای میانگین جامعه، برآوردی که در نمونه گیری طبقه ای استفاده می شود عبارتست از :
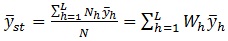
نمونه گیری گروهی دومرحله ای در واقع تعمیمی از مفهوم نمونه گیری خوشه ای است. یک خوشه عمدتاً مجموعه ای طبیعی یا مناسب از اعضا است، مانند بلوک هایی از خانوارها یا کارتون هایی از لامپ های تولید شده. هر خوشه ی مورد بررسی یا دارای تعداد اعضایی است بیش از آنچه که بتوان همه ی آن ها را مورد بررسی قرار داد و یا دارای اعضایی است که آن قدر مشابه هستند که اندازه گیری تعداد کمی از آن ها اطلاعاتی درباره ی تمام خوشه در اختیار ما قرار می دهد. در هریک از موارد ذکر شده ، پژوهشگر می تواند یک نمونه ی احتمالی از خوشه ها برگزیده و سپس یک نمونه ی احتمالی از اعضای درون هر خوشه انتخاب نماید.به این ترتیب یک نمونه ی خوشه ای دومرحله ای حاصل می شود. نمونه گیری احتمالی که در هر مرحله انجام می شود می تواند به کمک روش های مختلف نمونه گیری انجام شود. به دلیل کاربرد بیشتر نمونه گیری تصادفی ساده در ادامه نمونه گیری خوشه ای دو مرحله ای را با فرض آن که در هر مرحله نمونه ی مورد نظر با استفاه از روش تصادفی ساده حاصل شود ، بررسی می کنیم.
چند مثال کاربردی
1- یک بررسی ملی از نظرات دانشجویان، به وسیله انتخاب یک نمونه تصادفی ساده از دانشگاه های کشور و سپس انتخاب یک نمونه تصادفی ساده از دانشجویان هر دانشگاه انجام می شود. بنابراین هر دانشگاه متناظر با یک خوشه از دانشجویان است.
2- مقدار کل حساب های قابل وصول برای یک فروشگاه زنجیره ای را می توان ابتدا به وسیله ی گرفتن یک نمونه ی تصادفی ساده از فروشگاه ها و سپس انتخاب یک نمونه تصادفی ساده از حساب های هرکدام برآورد نمود. به این ترتیب هر فروشگاه زنجیره ای یک خوشه از حساب ها را فراهم می کند.
3- نمونه گیری برای اهداف کنترل کیفیت نیز اغلب شامل دو مرحله (یا بیشتر) است. برای مثال زمانی که یک بازرس از محصولات بسته بندی شده مانند غذای یخ زده نمونه گیری می کند، معمولا از میان کارتون ها تعدادی را انتخاب کرده و سپس از بسته های درون کارتون ها نمونه گیری می کند.
4- زمانی که نمونه گیری مستلزم وارسی مولفه های محصول ، مانند اندازه گیری ضخامت صفحه باطریهای اتومبیل است ، یک روند نمونه گیری عبارت است از نمونه برداری از برخی فرآورده ها (باطری ها) و سپس نمونه برداری از مولفه های (ضخامت) درون این فرآورده ها می باشد.
ایده ی اساسی نمونه گیری سیستماتیک انتخاب منظم تعدادی از افراد موجود در یک لیست می باشد. فرض کنید قرار است نمونه ای از اسم از فهرستی طولانی انتخاب شود.یک روش ساده برای این کار آن است که فاصله ای مناسب برگزیده و اسامی را در فواصل مساوی در طول فهرست انتخاب کنیم. اگر نقطه ی شروع برای این روند منظم انتخاب ، تصادفی باشد نتیجه یک نمونه گیری سیستماتیک است.به این ترتیب نمونه ای که به وسیله ی انتخاب یک عضو از بین اولین عضو یک فهرست ، سپس انتخاب هرامین عضو بعد از آن حاصل شود، یک نمونه تصادفی سیستماتیک 1 در K با شروع تصادفی نامیده می شود. اجرای روش نمونه گیری سیستماتیک اغلب آسان تر از تصادفی ساده است و همچنین امکان بروز خطا از طرف پرسشگر کاهش می یابد. برای مثال با استفاده از نمونه گیری تصادفی انتخاب نمونه به حجم n از خریداران واقع در بخشی از یک خیابان ، پرسشگر نمی تواند تعیین کند که کدام خریدار را در نمونه قرار دهد زیرا تا زمانی که تمام خریدارن از آن قسمت عبور نکرده اند اندازه ی جمعیت معلوم نیست. در مقابل پرسشگر می تواند یک نمونه ی سیستماتیک (مثلاً 1در 20) را تارسیدن به حجم نمونه ی مورد نظر اختیار کند.
علاوه بر آنچه گغته شد، نمونه گیری سیستماتیک اغلب اطلاعات بیشتری به ازای هزینه ی هر واحد از نمونه گیری تصادفی ساده ارائه می دهد. یک نمونه ی سیستماتیک به طور کلّی به صورت یکنواخت تر روی کلیه ی جمعیت توزیع می شود ودر نتیجه اطلاعات بیشتری درباره ی جامعه از یک جامعه نسبت به نمونه گیری تصادفی ساده با همان حجم بدست می دهد. برای مثال فرض کنید برای تعیین درصد پرونده هایی که نادرست بایگانی شده اند ، می خواهیم از بین 1000 پرونده نمونه ای به حجم 200 تهیه کنیم. حال اگر بدانیم 500 پرونده ی اول درست بوده و بعد به دلیل تغییر کارمند امکان اشتباه در پرونده های بعدی وجود دارد، استفاده از نمونه گیری تصادفی ساده مناسب نیست زیرا ممکن است تمام نمونه ها از پرونده های گروه اول یا دوم انتخاب شوند. در حالیکه نمونه گیری سیستماتیک تعداد مساوی از هردوگروه را انتخاب می کند. مثال های مختلفی برای استفاده از این نوع نمونه گیری وجود دارد مانند طرح های کنترل کیفیت صنعتی ، طرح های نظرسنجی از جمعیت های در حال حرکت و یا در نمونه گیری از کرت های مربوط به کشاورزی و ... .
برآورد میانگین و مقدار کل جامعه
از آنجاییکه هدف اغلب بررسی های نمونه ای برآورد یک یاچند پارامتر جامعه است. میانگین جامعه در نمونه گیری سیستماتیک به کمک میانگین نمونه برآورد می شود.
برآورد میانگین جامعه :
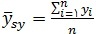
واریانس برآوردگر میانگین جامعه به صورت :
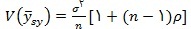
تعریف می شود که به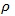
، ضریب همبستگی بین ازواج درون نمونه ی سیستماتیک ، بستگی دارد.اگر 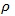به 1 نزدیک باشد ، اعضای درون نمونه نسبت به خصیصه ای که اندازه گیری می شود کاملا مشابه اند. و نمونه ی سیستماتیک واریانس بزرگی نسبت به نمونه گیری تصادفی ساده دارد.اگر منفی باشد یعنی اعضای درون یک نمونه کاملا متفاوت باشند ، نمونه گیری سیستماتیک ممکن است بهتر از تصادفی ساده باشد. برای 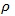های نزدیک به صفر و Nنسبتاً بزرگ این دو روش نمونه گیری تقریبا معادل اند.
نمونه گیری سیستماتیک در جوامع مختلف
در نمونه گیری سیستماتیک توجه به نوع قرار گرفتن اعضا در جامعه دارای اهمیت است. سه نوع جامعه ی مختلف را می توان در نظر گرفت ، جامعه تصادفی ، جامعه مرتّب شده و جامعه متناوب.
1.جامعه تصادفی : جامعه ای تصادفی است که اعضای آن دارای ترتیب خاصی نبوده و به صورت تصادفی قرار گرفته باشند. در نمونه ی سیستماتیک که از یک جامعه ی تصادفی انتخاب می شود انتظار می رود اعضای نمونه متجانس بوده و بنابراین مقدار 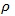صفر باشد. بنابراین زمانی که Nبزرگ است واریانس
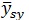تقریباً معادل واریانس
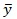براساس یک نمونه تصادفی ساده است. در این حالت نمونه گیری سیستماتیک و تصادفی ساده معادل اند. برای مثال یک پژوهشگر علاقمند است متوسط اقلام دارویی که توسط پزشکان معین در طول سال گذشته تجویز شده است ، تعیین نماید.اگر چارچوب شامل فهرست الفبایی از پزشکان باشد، این فرض که اسامی فهرست به تعداد اقلام دارویی وابسته نیست قابل قبول است (0=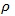) و بنابراین نمونه گیری سیستماتیک و تصادفی ساده معادل اند.
2.جامعه مرتب شده : جامعه ای مرتب است که اعضای آن نسبت به یک روش از نظر بزرگی مرتّب شده باشند. یک نمونه ی سیستماتیک برگرفته از جامعه ای مرتب به طور کلّی نامتجانس با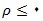
است .ثابت می شود که هرگاه N بزرگ و 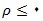باشد ،
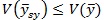است . بنابراین در یک جامعه ی مرتب یک نمونه ی سیستماتیک به ازای هر واحد هزینه اطلاعات بیشتری از نمونه گیری تصادفی ساده می دهد.
از آنجایی که ما نمی توانیم یک برآورد نااریب از نمونه ارائه دهیم یک برآورد نسبتاً خوب که البته بزرگتر از مقدار مورد انتظار است برای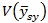 
عبارت است از :
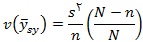
به عنوان یک مثال در این زمینه ، فرض کنید برای برآورد اثربخشی آموزش در یک کلاس درس عمومی از دانشجویان برای ارزیابی مدرّس براساس یک مقیاس عدی سوال می شود و یک نمونه از فهرست ارزیابی ها که از نظر عددی به صورت صعود ی مرتب شده است گرفته می شود. جامعه ی اندازه گیریهایی که نمونه از آن استخراج شده است به عنوان جامعه ی مرتب شده در نظر گرفته می شود.
3.جامعه ی تناوبی : جامعه ای تناوبی است که اعضای آن تغییرات دوره ای داشته باشند. برای مثال فرض کنید می خواهیم متوسط فروش روزانه ی خواروبار را در یک فروشگاه زنجیره ای محاسبه کنیم. از آنجایی که معمولاً حداکثر فروش در آخر هفته می باشد ، جامعه ی مورد نظر تناوبی است. موثر بودن یک نمونه ی 1 در k بستگی به مقداری دارد که برای k انتخاب می کنیم. اگر ما فروش روزانه را هر چهارشنبه بررسی کنیم احتمالا میانگین جامعه را کم برآورد خواهیم کرد. و یا اگر هر جمعه نمونه گیری کنیم، برآورد مورد نظر بیش از حد واقعی خواهد بود. در چنین حالتی می توان نمونه گیری را مثلا هر 9 روز یک بار انجام داد. به این ترتیب از تمام روزها با فروش زیاد و کم نمونه گیری به عمل خواهد آمد.
اعضای یک نمونه ی سیستماتیک که از جامعه ی تناوبی به دست آمده است می تواند متجانس باشد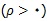 
. در این حالت نیز ثابت می شود اگر N بزرگ باشد و 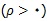آن گاه :
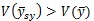
بنابراین نمونه گیری سیستماتیک به ازای هر واحد هزینه ، اطلاعات کمتری از نمونه ی تصادفی ساده فراهم می آورد. از آنجایی که واریانس نمونه گیری سیستماتیک در این حالت نیز قابل محاسبه نمی باشد ، این واریانس به کمک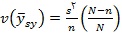 
برآورد می شود که البته این برآوردگر مقداری کمتر از مقدار واقعی را برآورد می کند.
برای جلوگیری از این مشکل که با نمونه گیری از جامعه تناوبی بوجود می آید ، پژوهشگر باید نقطه ی شروع تصادفی را چندین بار تغییر دهد. این روش احتمال انتخاب مشاهدات از موقعیت نسبی یکسان را کاهش می دهد. روش انتخاب چند نقطه ی شروع تصادفی در طول نمونه ی سیستماتیک ، اثر به هم ریختن اعضای جامعه و سپس انتخاب یک نمونه ی سیستماتیک را دارد.
انتخاب حجم نمونه
برای بدست آوردن تعداد مشاهدات لازم برای برآورد میانگین جامعه با حداکثر خطای Bاز رابطه ی زیر
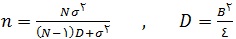
استفاده می کنیم.
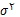با استفاده از اطلاعاتی که از تحقیقات مشابه پیشین بدست آمده و یا به کمک یک نمونه ی اولیه قابل محاسبه است.
منبع : مقدمه ای بربررسی های نمونه ای . نوشته ی شیفر و مندنهال. ترجمه ی دکتر ارقامی ، دکتر بزرگنیا و دکتر سنجری . انتشارات دانشگاه فردوسی مشهد.
در میان روش های نمونه گیری با احتمالات برابر، روش نمونه گیری تصادفی ساده یکی از ساده ترین و قدیمی ترین روش های نمونه گیری است که در عمل کاربرد بسیاری دارد. اگر نمونه ای به حجم از جامعه ای به حجم به گونه ای انتخاب شود که هر نمونه ی ممکن تایی شانس یکسان برای انتخاب شدن داشته باشد ، آن را نمونه گیری تصادفی ساده می نامند. نمونه گیری تصادفی ساده به دو روش نمونه گیری با جایگذاری و نمونه گیری بدون جایگذاری قابل اجرا می باشد اما در عمل نمونه گیری با جایگذاری کاربرد چندانی ندارد .
مجموعه واحدهائی که حداقل در یک صفت مشترک باشند یک جامعه آماری را تشکیل می‌دهند. نمونه آماری نیز عبارت است از مجموعه ای نشانه‌ها که از یک قسمت، گروه یا جامعه‌ای بزرگتر انتخاب می‌شود، به طوری که این مجموعه معرف کیفیات و ویژگیهای آن قسمت، گروه یا جامعه بزرگتر باشند و نمونه گیری فرایند انتخاب نمونه است. (خاکی، 1378) فرمول‌های تعیین اندازه نمونه متفاوت است. یکی از روشهای پرکاربرد در تعیین حجم نمونه فرمول کوکران است. فرمول کوکران به‌صورت زیر محاسبه می‌شود:
نمونه گیری در پژوهش های کیفی و کمی تفاوت بسیار دارد زیرا هدف آن به جای تعمیم یافت هها، کسب درک عمیق از پدیده مورد بررسی است. انتخاب مشارکت کنندگان در پژوهش کیفی با هدف دستیابی به بیشترین اطلاعات در مورد پدیده مورد بررسی انجام می‌شود. در پژوهش کمی تأکید بسیار زیادی بر انتخاب تصادفی شانس برابر برای انتخاب همه اعضای جامعه پژوهش وجود دارد اما در پژوهش کیفی نمونه پژوهش یا مشارکت کنندگان، انتخاب یا دعوت می شوند. نمونه‌گیری هدفمند که نمونه‌گیری غیراحتمالی، هدفدار یا کیفی نیز نامیده می‌شود به معنای انتخاب هدف دار واحدهای پژوهش برای کسب دانش یا اطلاعات است. این نوع نمونه‌گیری به دنبال ایجاد قوانین ثابت و تغییرناپذیر و یا تعمیم نتایج نیست بلکه سعی در شناخت بهتر هر پدیده در زمینه خاص دارد. سه نوع عمده نمونه‌گیری هدفمند شامل نمونه‌گیری برای رسیدن به معرف بودن یا قابلیت مقایسه، نمونه گیری موارد خاص یا یگانه و نمونه‌گیری متوالی هستند. استفاده از روش اشباع داده در پژوهش های کیفی به عنوان استاندارد طلایی پایان نمونه‌گیری در نظر گرفته می‌شود. در این مقاله سعی شد روشهای انتخاب مشارکتک‌نندگان و تفاو تهای رو شهای کمی و کیفی معرفی شود و راهکاری برای تصمیم‌گیری در مورد رسیدن به اشباع داده ارائه گردد.
منبع: هادی رنجبر و همکاران، پائیز ۱۳۹۱
یک سوال بسیار بااهمیت در تحلیل عاملی تعیین حداقل حجم نمونه است. (کلاین، 1990) تعیین حداقل حجم نمونه لازم برای گردآوری داده‌های مربوط به مدلیابی معادلات ساختاری بسیار با اهمیت است. (مک‌کیتی، 2004) با وجود آنکه در مورد حجم نمونه لازم برای تحلیل عاملی و مدل‌های ساختاری توافق کلی وجود ندارد (شریبر، 2006)، اما به زعم بسیاری از پژوهشگران حداقل حجم نمونه لازم 200 می‌باشد. (هولتر، 1983؛ گارور و منتزر، 1999؛ سیوو و همکاران، 2006؛ هو، 2008) کلاین نیز معتقد در تحلیل عاملی اکتشافی برای هر متغیر 10 یا 20 نمونه لازم است اما حداقل حجم نمونه 200 قابل دفاع است. (کلاین، 2010)
اما در تحلیل عاملی تائیدی حداقل حجم نمونه براساس عامل‌ها تعیین می‌شود نه متغیرها. اگر از مدلیابی معادلات ساختاری استفاده شود حدود 20 نمونه برای هر عامل (متغیر پنهان) لازم است. (جکسون، 2003) حجم نمونه توصیه شده برای تحلیل عامل تائیدی حدود 200 نمونه برای ده عامل توصیه شده است. (شه و گلداشتاین، 2006، کلاین، 2010)
ساختار کلی تحلیل عاملی تائیدی؛ منبع: حبیبی، ۱۳۹۱ ص ۱۳
مثال کاربردی
فرض کنید یک پرسشنامه شامل ۷ گویه برای سنجش سازه A طراحی کرده‌اید. چنانچه هیچ پیش فرضی درباره ابعاد (متغیرهای پنهان) سازه A نداشته باشید با استفاده از تحلیل عاملی اکتشافی می توانید ابعاد سازه A را شناسائی کنید. برای منظور چون ۷ گویه موجود است بنابراین به حداقل ۷۰ و حداکثر ۱۴۰ نمونه نیاز دارید تا ساختار علی متغیرهای مدل شناسائی شود. اما اگر براساس ادبیات پژوهش یا مصاحبه با خبرگان و ... ابعاد سازه مورد بررسی تعیین شده باشد و برای مثال مانند شکل بالا دو متغیر پنهان B و C برای این سازه در نظر گرفته شده باشد در این صورت از تحلیل عاملی تائیدی استفاده خواهد شد. در این حالت چون ۲ متغیر پنهان وجود دارد به حداکثر ۴۰ نمونه نیاز دارید تا ساختار علی متغیرهای مدل تائید شود.
جدولی که به نام جدول مورگان معروف است یکی از پرکاربردترین روش‌ها برای محاسبه حجم نمونه آماری است. جدول مورگان در واقع حاصل زحماتی است که robert v. krejcie و daryle w. morgan کشیده اند و به ازای مقادیر مختلف از اندازه های جامعه با استفاده از فرمول کوکران نمونه را برآورد کرده اند. یعنی شما هر یک از اعداد این جدول را در فرمول کوکران بگدارید همین حجم نمونه را مشاهده خواهید کرد. برای آزمون این ادعا اعداد این جدول را در فرمولی که توسط سایت پارس مدیر در بحث محاسبه آنلاین حجم نمونه برنامه نویسی شده است وارد کنید. نتیجه را خودتان مشاهده خواهید کرد. بنابراین جدول کرجشس و مورگان چیزی جز همان کاربرد فرمول کورکان نیست.
| N | S | N | S | N | S | N | S | N | S |
| 10 | 10 | 100 | 80 | 280 | 162 | 800 | 260 | 2800 | 338 |
| 15 | 14 | 110 | 86 | 290 | 165 | 850 | 265 | 3000 | 341 |
| 20 | 19 | 120 | 92 | 300 | 169 | 900 | 269 | 3500 | 246 |
| 25 | 24 | 130 | 97 | 320 | 175 | 950 | 274 | 4000 | 351 |
| 30 | 28 | 140 | 103 | 340 | 181 | 1000 | 278 | 4500 | 351 |
| 35 | 32 | 150 | 108 | 360 | 186 | 1100 | 285 | 5000 | 357 |
| 40 | 36 | 160 | 113 | 380 | 181 | 1200 | 291 | 6000 | 361 |
| 45 | 40 | 180 | 118 | 400 | 196 | 1300 | 297 | 7000 | 364 |
| 50 | 44 | 190 | 123 | 420 | 201 | 1400 | 302 | 8000 | 367 |
| 55 | 48 | 200 | 127 | 440 | 205 | 1500 | 306 | 9000 | 368 |
| 60 | 52 | 210 | 132 | 460 | 210 | 1600 | 310 | 10000 | 373 |
| 65 | 56 | 220 | 136 | 480 | 214 | 1700 | 313 | 15000 | 375 |
| 70 | 59 | 230 | 140 | 500 | 217 | 1800 | 317 | 20000 | 377 |
| 75 | 63 | 240 | 144 | 550 | 225 | 1900 | 320 | 30000 | 379 |
| 80 | 66 | 250 | 148 | 600 | 234 | 2000 | 322 | 40000 | 380 |
| 85 | 70 | 260 | 152 | 650 | 242 | 2200 | 327 | 50000 | 381 |
| 90 | 73 | 270 | 155 | 700 | 248 | 2400 | 331 | 75000 | 382 |
| 95 | 76 | 270 | 159 | 750 | 256 | 2600 | 335 | 100000 | 384 |